二分图#

定义#

二分图#

对于一个无向图 $G=(V, E)$，可以将 $V$ 分为两个不相交的子集，使得任意一条边的顶点分属两个不同的点集，那么这个无向图是二分图。

匹配#

对于无向图 $G=(V, E)$，取边集的子集 $E^*$，使得 $E^*$ 中任意两条边没有公共顶点，那么 $E^*$ 是图 $G$ 的一个匹配，又称边独立集。

最大匹配#

边数最多的匹配。极大匹配的边数唯一，取法可能不唯一。

匹配边 & 非匹配边#

在边独立集中的边是匹配边，反之是非匹配边。

匹配点 & 非匹配点#

能被匹配边连接到的点是匹配点，反之是非匹配点。

完美匹配#

若 $M$ 是图 $G$ 的一个匹配，且 $G$ 中的每个顶点都是匹配点，那么 $M$ 是 $G$ 的完美匹配。

交错路径#

图 $G$ 中，由匹配边和非匹配边交替构成的路径，是交错路径。

增广路径#

起点和终点都是非匹配点的交错路径，是增广路径。

显然，$M$ 是 $G$ 的最大匹配，当且仅当 $G$ 中不含关于 $M$ 的增广路径。

因为如果 $G$ 中含有关于 $M$ 的增广路径，把增广路径上的匹配边取反，可以使匹配大小增加$1$.

二分图最大匹配#

概述#

在二分图中找到一个最大匹配。

Hall定理#

二分图 $G=<V_1, V_2, E>$，其中 $|V_1| \leq |V_2|$，则 $G$ 中存在 $V_1$ 到 $V_2$ 的完美匹配，当且仅当 $V_1$ 中任意 $k\in [1, |V_1|]$ 个顶点，都至少与 $V_2$ 中的 $k$ 个顶点相连。

反证即可。

思想#

对一条增广路进行异或之后，能使匹配中的边数增加 $1$.

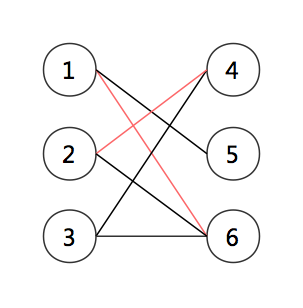
异或之后，可以得到：

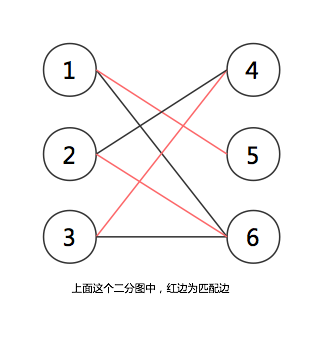
匈牙利算法#

1. 将初始的匹配 $M$ 置为 $\emptyset$.
2. 找到一条增广路径，通过异或操作更新最大匹配。
3. 重复2.

时间复杂度：$\mathcal{O}(EV)$

代码（From Jisuanke）：

const int MAX_N = 100;
const int MAX_M = 10000;
struct Edge {
    int v, next;
} e[MAX_M];
int p[MAX_N], eid;
void init() {
    memset(p, -1, sizeof(p));
    eid = 0;
}
void insert(int u, int v) {
    e[eid].v = v;
    e[eid].next = p[u];
    p[u] = eid++;
}
bool vst[MAX_N];
int rmatch[MAX_N];
bool dfs(int u) {
    for(int i = p[u]; i != -1; i = e[i].next) {
        int v = e[i].v;
        if(!vst[v]) {
            vst[v] = true;
        	if(rmatch[v] == -1 || dfs(rmatch[v])) {
                rmatch[v] = u;
                return true;
            }
        }
    }
    return false;
}
int hungary(int n) {
    int cnt = 0;
    memset(rmatch, -1, sizeof(rmatch));
    for(int i = 1; i <= n; i++) {
        memset(vst, 0, sizeof(vst));
        cnt += dfs(i);
    }
    return cnt;
}