斜率优化DP#

五道题，套路基本相同，~~期望2h讲完~~.

P3195 - 玩具装箱#

题意#

有 $n$ 个玩具，第 $i$ 个玩具价值为 $c_i$ 。要求将这 $n$ 个玩具排成一排，分成若干段。对于一段 $[l,r]$ ，它的代价为：

(r-l+\sum_{i=l}^r c_i-L)^2

求分段的最小代价。

$1\le n\le 5\times 10^4,1\le L,0\le c_i\le 10^7$ .

DP#

令 $f_i$ 表示前 $i$ 个物品，分若干段的最小代价。

状态转移方程：

f_i=\min_{j<i}{\{f_j+(pre_i-pre_j+i-j-1-L)^2\}}

其中 $pre_i$ 表示 $c$ 数列中，前 $i$ 个数的和，即 $\sum_{j=1}^i c_j$ 。

时间复杂度为 $O(n^2)$ ，无法解决本题。

优化#

简化状态转移方程式：令 $s_i=pre_i+i,L'=L+1$ ，则

f_i=\min_{j<i}{f_j+(s_i-s_j-L')^2}

我们目前优化的目的，是尽快地找到上面式子中的 $j$ ，也就是令 $f_i$ 最小化的继承状态。

为了表示方便，设 $j$ 为能使 $f_i$ 最小化的继承状态，所以有：

f_i=f_j+(s_i-s_j-L')^2

考虑一次函数的斜截式 $y=kx+b$ ，将方程转化为这个形式。

其中变量 $x, y$ 与 $j$ 有关， $b, k$ 与 $j$ 无关，且要求 $x$ 随 $j$ 单调递增， $b$ 中包含 $f_i$ （建模需要）。

按照上面的规则，对方程进行整理：

\begin{aligned} f_i&=f_j+[s_i-(s_j+L')]^2\\ f_i&=f_j+{s_i}^2-2s_i(s_j+L')+(s_j+L')^2\\ f_i-{s_i}^2+2s_i(s_j+L')&=f_j+(s_j+L')^2\\ \end{aligned}

也就是：

f_j+(s_j+L')^2=2s_i(s_j+L)+f_i-{s_i}^2

与一次函数 $y=kx+b$ 对照地看，其中：

\left\{ \begin{array}{**lr**} y = f_j+(s_j+L')^2\\ k = 2s_i\\ x = s_j+L\\ b = f_i-{s_i}^2 \end{array} \right.

我们把 $(x, y)$ 看成平面直角坐标系上的点。那么现在 $(x_j, y_j)$ 的意义就是：直线 $y=kx+b$ 上的一个点。

又因为我们的目的是最小化 $f_i$ ，在上面的表示当中， $f_i$ 只与直线的截距 $b$ 有关。所以显然地，问题转化为：如何选取 $j$ ，才能使得过点 $(x_j, y_j)$ 的直线的截距 $b$ 最小。

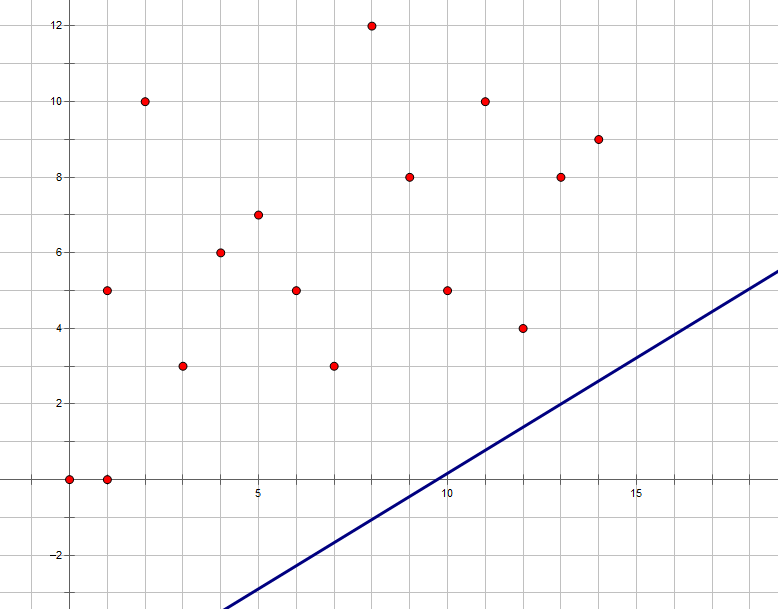
注意到：直线的斜率不变。于是相当于平移直线 $y=kx$ ，直到其经过图中的一个点。

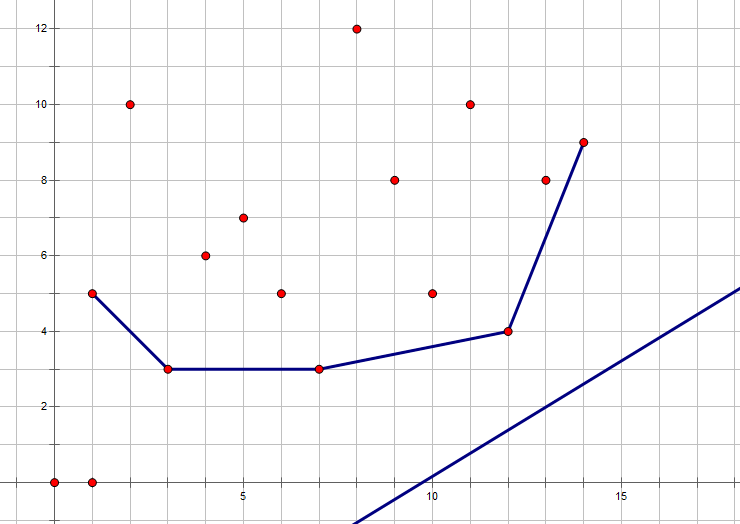
20190701195640154

如图，为了最小化 $b$ ，显然除了折线上面的点，都不可能是最优解。（这条折线上的点集就是凸包的一部分。

在折线上任取三个点 $A, B, C$ 满足 $x_A<x_B<x_C$ ，一定满足 $\operatorname{slope}(A,B)<\operatorname{slope}(B, C)$ .

由图像又易知，最优解 $j$ 就是第一个 $\operatorname{slope}(j, j+1)>k$ 的点。

于是可以得到 $\mathcal{O}(n\log n)$ 的算法。（处理凸包后，每次利用单调性二分）

由于随着 $i$ 的增长， $k=2s_i$ 也是单调递增的，不难发现可以用单调队列得到 $\mathcal{O}(n)$ 的算法。

设单调队列（递增）为 $q$ ，队首为 $head$ ，队尾为 $tail$ ，当前要转移 $i$ 号点，那么具体步骤：

当 $\operatorname{slope}(q_{head}, q_{head+1})\leq2 s_i$ 时， $head$ ++，（保证最优解）
此时的 $q_{head}$ 就是最优转移点，根据它和转移方程计算出 $f_i$ ，
当 $\operatorname{slope}(q_{tail-1}, q_{tail})\geq\operatorname{slope}(q_{tail}, i)$ 时， $tail$ —，（维护下凸包）
在队尾插入 $i$ .

图 ↗

代码#

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 5e4 + 10;
int n, L;
int c[MAXN], s[MAXN], f[MAXN];
double slope(int i, int j) {
	return ((f[j]+(s[j]+L)*(s[j]+L)) - (f[i]+(s[i]+L)*(s[i]+L))) / (double)(s[j] - s[i]);
}
int head, tail, q[MAXN];
signed main() {
	scanf("%lld%lld", &n, &L);
	L += 1;
	for(int i = 1; i <= n; i++) {
		scanf("%lld", &c[i]);
		s[i] = s[i - 1] + c[i] + 1;
	}
	head = tail = 1;
	for(int i = 1; i <= n; i++) {
		while(head < tail && slope(q[head], q[head + 1]) <= 2 * s[i]) {
            head++;
        }
		f[i] = f[q[head]] + (s[i] - s[q[head]] - L) * (s[i] - s[q[head]] - L);
		while(head < tail && slope(q[tail - 1], q[tail]) >= slope(q[tail], i)) {
            tail--;
        }
		q[++tail] = i;
	}
	printf("%lld", f[n]);
	return 0;
}

P3628 [APIO2010]特别行动队#

题目描述#

你有一支由 $n$ 名预备役士兵组成的部队，士兵从 $1$ 到 $n$ 编号，你要将他们拆分成若干特别行动队调入战场。出于默契的考虑，同一支特别行动队中队员的编号应该连续，即为形如 $(i, i + 1,\cdots, i+k)$ 的序列。所有的队员都应该属于且仅属于一支特别行动队。

编号为 $i$ 的士兵的初始战斗力为 $x_i$ ，一支特别行动队的初始战斗力 $X$ 为队内士兵初始战斗力之和，即 $x_i + x_{i+1} + \cdots + x_{i + k}$ .

通过长期的观察，你总结出对于一支初始战斗力为 $X$ 的特别行动队，其修正战斗力 $X'=aX^2+bX+c$ ，其中 $a, b, c$ 是已知的系数 $a < 0$ . 作为部队统帅，现在你要为这支部队进行编队，使得所有特别行动队的修正战斗力之和最大。

试求出这个最大和。

$1\leq n\leq 10^6, -5\leq a\leq -1, -10^7\leq b, c\leq 10^7, 1\leq x_i\leq 100$ .

DP#

与上一题类似。

令 $f_i$ 表示前 $i$ 个物品，分若干段的最小代价，有状态转移方程：

f_i=\max_{j<i}{\{f_j+a(s_i-s_j)^2+b(s_i-s_j)+c\}}

其中 $s_i$ 是 $x$ 数列的前缀和，也就是 $s_i=\sum_{j=1}^i{x_j}$ .

优化#

设 $j$ 是能使 $f_i$ 最大化的继承状态，那么整理状态转移方程：

\begin{aligned} f_i&=f_j+a(s_i-s_j)^2+b_(s_i-s_j)+c\\ f_i&=f_j+a({s_i}^2+{s_j}^2-2s_is_j)+b(s_i-s_j)+c\\ f_i&=f_j+a\cdot {s_i}^2+a\cdot {s_j}^2-2a\cdot s_is_j+b\cdot s_i-b\cdot s_j+c \end{aligned}

考虑一次函数斜截式 $y=kx+b$ 或 $b=y-kx$ ，将状态转移方程变换为这个形式。

其中变量 $x, y$ 与 $j$ 有关， $b, k$ 与 $j$ 无关。

\textcolor{red}{f_i-b\cdot s_i-a\cdot {s_i}^2}=\textcolor{purple}{(f_j+a\cdot {s_j}^2-b\cdot s_j+c)}-\textcolor{green}{2a\cdot s_i}\textcolor{blue}{s_j}

所以：

\left\{ \begin{array}{lr} y = f_j+a\cdot {s_j}^2-b\cdot s_j+c\\ k = 2a\cdot s_i\\ x = s_j\\ b = f_i-b\cdot s_i-a\cdot {s_i}^2 \end{array} \right.

要最大化 $f_i$ ，也就是最大化截距 $b$ ，把 $(x_j, y_j)$ 看作平面直角坐标系上的点。

那么由于本题中 $k=2as_i$ ，是单调递减的，与上凸包单调性相同。所以与上一题类似，选取的点一定只在上凸包上，并且是第一个斜率小于 $k$ 的点。

可以用单调队列维护：

设单调队列（递增）为 $q$ ，队首为 $head$ ，队尾为 $tail$ ，当前要转移 $i$ 号点，那么具体步骤：

当 $\operatorname{slope}(q_{head}, q_{head+1})\textcolor{red}{\geq}2a\cdot s_i$ 时， $head$ ++，（保证最优解）
此时的 $q_{head}$ 就是最优转移点，根据它和转移方程计算出 $f_i$ ，
当 $\operatorname{slope}(q_{tail-1}, q_{tail})\textcolor{red}{\leq}\operatorname{slope}(q_{tail}, i)$ 时， $tail$ —，（维护上凸包）
在队尾插入 $i$ .

代码#

#include <bits/stdc++.h>
#define int long long
#define x(X) (s[X])
#define y(X) (f[X] + a * s[X] * s[X] - b * s[X] + c)
using namespace std;
const int MAXN = 1e6 + 10;
int n;
int a, b, c;
int s[MAXN], f[MAXN];
int head, tail, q[MAXN];
double slope(int i, int j) {
	return 1.0 * (y(j) - y(i)) / (x(j) - x(i));
}
signed main() {
	scanf("%lld%lld%lld%lld", &n, &a, &b, &c);
	for(int i = 1; i <= n; i++) {
		int tmp; scanf("%lld", &tmp);
		s[i] = s[i - 1] + tmp;
	}
	head = tail = 1;
	for(int i = 1; i <= n; i++) {
		while(head < tail && slope(q[head], q[head + 1]) >= 2ll * a * s[i]) {
            head++;
        }
		int j = q[head]; f[i] = f[j] + a * (s[i]-s[j])*(s[i]-s[j]) + b * (s[i]-s[j]) + c;
		while(head < tail && slope(q[tail - 1], q[tail]) <= slope(q[tail], i)) {
            tail--;
        }
		q[++tail] = i;
	}
	cout << f[n] << endl;
	return 0;
}

P3648 [APIO2014]序列分割#

题目描述#

你正在玩一个关于长度为 $n$ 的非负整数序列的游戏，序列中第 $i$ 个元素的值为 $a_i$ . 这个游戏中，你需要把序列分为 $k+1$ 个非空的块。为了得到 $k+1$ 块，你需要重复下面的操作 $k$ 次：

选择一个有超过一个元素的块（初始时你只有一块，即整个序列）
选择两个相邻元素，把这个块从中间分开，得到两个非空的块。

每次操作后，你将获得那两个新产生的块的元素和的乘积的分数。

求总得分最大值，并输出任意一种分割方案。

$2\leq n\leq 10^5, 1\leq k\leq \min{\{n-1, 200\}}$ .

分析#

首先可以发现，最终的分数与切的顺序无关。

证明：对于长度为 $3$ 的序列 $xyz$ ，将其分为三部分，只有两种方法：

先分割 $xy$ ，再分割 $yz$ ，贡献为 $x(y+z)+yz=xy + yz + xz$ ，
先分割 $yz$ ，再分割 $xy$ ，贡献为 $(x+y)z + xy=xy+yz+xz$ .

显然可以推广到更大的长度，于是结论得证。

DP#

由于上面的结论，假设所有切割是按照从左到右的顺序进行的。

定义 $\operatorname{DP}_{i, j}$ 表示前 $i$ 个数，进行了 $j$ 次切割的最大得分，那么有状态转移方程：

\operatorname{DP}_{i, k}=\max_{j<i}{\{\operatorname{DP}_{j, k-1}+s_j(s_i-s_j)\}}

其中 $s$ 是题目序列中的元素前缀和，即 $s_i=\sum_{j=1}^{i}a_j$ .

优化#

考虑到斜率优化的形式，需要 $\operatorname{DP}$ 变成一维，又发现状态转移方程中， $\operatorname{DP}_i$ 只和 $\operatorname{DP}_{i-1}$ 有关，所以可以滚动数组。

设 $f_i=\operatorname{DP}_{i, k}$ ， $g_j=\operatorname{DP}_{j, k-1}$ ，那么方程可以写为：

f_i=\max_{j<i}{\{g_j+s_j(s_i-s_j)\}}

这就很容易想到斜率优化。

设 $j$ 是能使 $f_i$ 最大化的继承状态，那么状态转移方程化为：

f_i=g_j+s_j(s_i-s_j)

考虑一次函数斜截式 $y=kx+b$ ，要把方程转化为这个形式。

其中变量 $x, y$ 与 $j$ 相关，常量 $b, k$ 与 $j$ 无关。

于是：

\begin{aligned} f_i&=g_j+s_j(s_i-s_j)\\ f_i&=g_j+s_is_j-{s_j}^2\\ g_j-{s_j}^2&=-s_is_j+f_i \end{aligned}

所以：

\left\{ \begin{array}{**lr**} y = g_j-{s_j}^2\\ k = -s_i\\ x = s_j\\ b = f_i \end{array} \right.

这里斜率 $k$ 是单调下降的，并且最优决策点 $(x_j, y_j)$ 是第一个满足 $\operatorname{slope}(j, j+1) < k$ 的点。所以最优决策点一定在上凸包上。

#include <bits/stdc++.h>
#define int long long
#define X(i) (s[i])
#define Y(i) (g[i] - s[i] * s[i])
using namespace std;
const long double inf = -1e18;
const int MAXN = 1e5 + 10;
int n, k;
int s[MAXN], f[MAXN], g[MAXN];
double slope(int i, int j) {
	if(s[j] == s[i]) return inf;
	return (Y(j) - Y(i)) / (double)(X(j) - X(i));
}
int head, tail, q[MAXN];
int to[210][MAXN];
signed main() {
	scanf("%lld%lld", &n, &k);
	for(int i = 1; i <= n; i++) {
		int tmp; scanf("%lld", &tmp);
		s[i] = s[i - 1] + tmp;
	}
	for(int l = 1; l <= k; l++) {
		head = tail = 1; q[1] = 0;
		for(int i = 1; i <= n; i++) {
			while(head < tail && slope(q[head], q[head + 1]) >= -1 * s[i]) {
                ++head;
            }
			int j = q[head]; to[l][i] = q[head];
			f[i] = g[j] + s[j] * (s[i] - s[j]);
			while(head < tail && slope(q[tail - 1], q[tail]) <= slope(q[tail], i)) { 
                tail--;
            }
			q[++tail] = i;
		}
		memcpy(g, f, sizeof(f));//把f复制到g
	}
	printf("%lld\n", f[n]);
	for(int i = k, j = n; i >= 1; i--) {
		j = to[i][j];
		printf("%lld ", j);
	}
	return 0;
}

P4360 [CEOI2004]锯木厂选址#

题目描述#

从山顶到山底下沿着一条直线种植了 $n$ 颗老树。当地的政府决定把它们砍下来。为了不浪费任何一颗木材，树被砍倒后要运送到锯木厂。

木材只能朝山下运。山脚下有一个锯木厂。另外两个锯木厂将新修建在山路上。你必须决定在哪里修建这两个锯木厂，使得运输的费用总和最小。假定运输每公斤木材，移动每米需要一分钱。

题目给定第 $i$ 颗树的重量 $w_i$ ，以及第 $i$ 颗树与第 $i+1$ 颗树之间的距离 $d_i$ .

请计算最小运输费用。

$2\leq n\leq 20000, 1\leq w_i, d_i\leq 10000$ ，保证在 long long 范围内。

DP#

https://blog.csdn.net/forever_dreams/article/details/97973474 ↗

这题难点可能在这部分…）

定义 $f_i$ 为以 $i$ 作为第二个锯木厂的最小花费， $s_i$ 为 $w_i$ 的前缀和， $dis_i$ 为 $d_i$ 的后缀和， $cost$ 为 $w_i\times dis_i$ 的总和。

转移就是通过枚举第一个锯木厂，然后减去省掉的花费。有下面的转移方程：

f_i=\min_{j<i}{\{cost - s_j\times dis_j-(s_i-s_j)\times dis_i\}}

斜率优化#

这部分和前面都一样，所以字越来越少……

设 $j$ 最优，化简：

\begin{aligned} f_i&=cost-s_j\times dis_j-s_i\times dis_i+s_j\times dis_i\\ s_j\times dis_j&=s_j\times dis_i+(cost-f_i-s_i\times dis_i) \end{aligned}

所以：

\left\{ \begin{array}{**lr**} y = s_j\times dis_j\\ k = dis_i\\ x = s_j\\ b = cost-f_i-s_i\times dis_i \end{array} \right.

$k=dis_i$ 是后缀和，单调递减。又因为要最小化 $f_i$ ，所以要最大化 $b$ 。

所以最优决策点 $(x_j, y_j)$ 是第一个满足 $\operatorname{slope}(j, j+1)<k$ 的点，单调队列维护上凸包即可。

代码#

#include <bits/stdc++.h>
#define int long long
#define X(i) (s[i])
#define Y(i) (s[i] * dis[i])
using namespace std;
const int MAXN = 2e4 + 10;
int n;
int w[MAXN], d[MAXN];
int cost, s[MAXN], dis[MAXN], f[MAXN];
double slope(int i, int j) {
	return (Y(j) - Y(i)) / (double)(X(j) - X(i));
}
int head, tail, q[MAXN];
int ans = 1e18;
signed main() {
	scanf("%lld", &n);
	for(int i = 1; i <= n; i++) scanf("%lld%lld", &w[i], &d[i]);
	for(int i = 1; i <= n; i++) s[i] = s[i - 1] + w[i];
	for(int i = n; i >= 1; i--) dis[i] = dis[i + 1] + d[i];
	for(int i = 1; i <= n; i++) cost += w[i] * dis[i];
	head = tail = 1;
	for(int i = 1; i <= n; i++) {
		while(head < tail && slope(q[head], q[head + 1]) >= dis[i]) ++head;
		int j = q[head];
		f[i] = cost - s[j] * dis[j] - (s[i] - s[j]) * dis[i];
		ans = min(ans, f[i]);
		while(head < tail && slope(q[tail - 1], q[tail]) <= slope(q[tail], i)) tail--;
		q[++tail] = i;
	}
	printf("%lld\n", ans);
	return 0;
}

P2900 [USACO08MAR]Land Acquisition G#

题目描述#

翻译的不是很好，所以我简化一下题面。

给定 $n$ 个矩阵的宽 $w$ 和高 $h$ ，每次选一个矩阵集合，代价为集合中的 $\max{\{w\}}\times \max{\{h\}}$ 。

任意两次之间没有重复的矩阵，求取完所有矩阵的最小代价。

分析#

注意到对于两个矩阵 $i, j$ ，如果 $w_i\leq w_j$ 并且 $h_i\leq h_j$ ，那么 $i$ 和 $j$ 一定可以放到一组， $i$ 对答案没有贡献，不用考虑，可以直接删去。

比如下图当中的 $1$ 和 $2$ . 矩阵 $2$ 能完全被 $1$ 包含，所以 $2$ 没有贡献，可以删去。

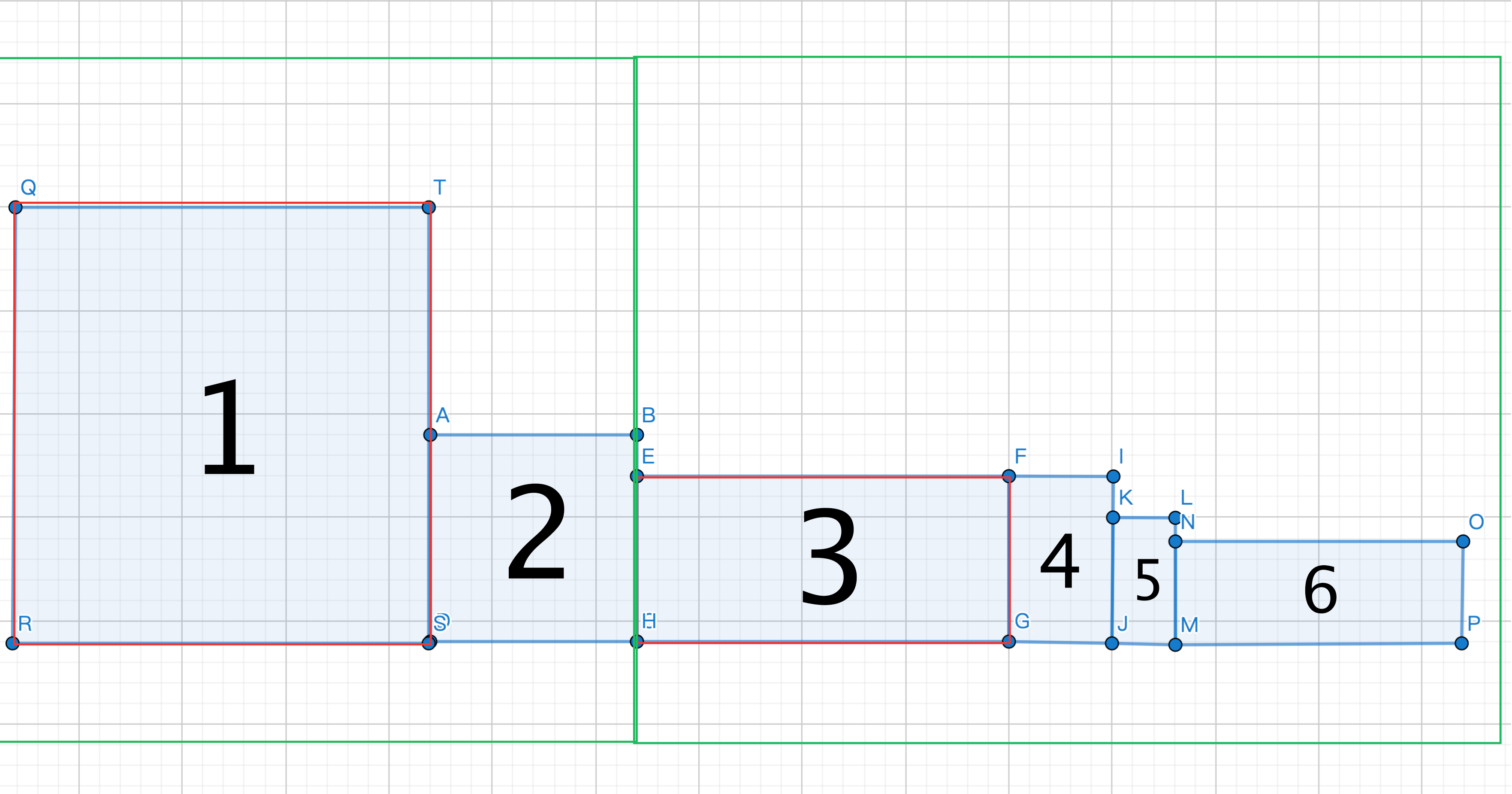
P2900-1

于是考虑先删除所有 $i$ 这样的矩阵。

具体做法就是：按照 $h$ 为第一关键字， $w$ 为第二关键字从大到小排序，之后双指针扫一遍即可。

//a已经降序排序
int t = 0;
for(int i = 1; i <= n; i++) {
	if(a[i].w > a[t].w) a[++t] = a[i];
}

cpp

如上图，剩下的只有 $1, 3$ 号矩阵。

删完之后剩下的就是一个， $h$ 严格单调递减， $w$ 严格单调递增的序列。考虑 $DP$ 解决。

DP#

设 $f_i$ 为新序列中，取走前 $i$ 个矩阵的最小花费， $w$ 为宽（单调递增）， $h$ 为高（单调递减），那么有转移方程：

f_i=\min_{j=0}^{i}{\{f_{j}+w_ih_{j+1}\}}

相当于，把 $j+1$ 到 $i$ 这一段合为一组取走。由于单调性，所以这一组的 $\max{\{w\}}=w_i$ ， $\max{\{h\}}=h_{j+1}$ .

复杂度 $\mathcal{O}(n^2)$ 。这显然可以斜率优化。

斜率优化#

我们目前优化的目的，是尽快地找到 $f_i$ 到底是由哪个 $j$ 转移过来的，也就是尽快找到最小化 $f_i$ 的继承状态。

为了表示方便，设 $j$ 为能使 $f_i$ 最小化的继承状态，所以有：

f_i=f_{j}+w_ih_{j+1}

考虑一次函数斜截式 $y=kx+b$ 或 $b=y-kx$ ，将状态转移方程变换为这个形式：

f_{j}=-w_ih_{j+1}+f_i

其中变量 $x, y$ 与 $j$ 有关， $b, k$ 与 $j$ 无关。且要求 $x$ 随 $j$ 单调递增， $b$ 中包含 $f_i$ （斜率优化基本操作）。

所以可以构造出直线方程为：

\left\{ \begin{array}{**lr**} y = f_j\\ k = w_i\\ x = -h_{j+1}\\ b = f_i \end{array} \right.

$x$ 随 $j$ 单调递增， $k$ 随 $i$ 单调递增，要使截距 $b=f_i$ 最小，最优解 $j$ 就是从左往右枚举到的第一个 $\operatorname{slope}(j, j+1)>k$ 的点。

所以单调队列维护下凸包即可。

代码#

#include <bits/stdc++.h>
#define X(i) (-a[i+1].h)
#define Y(i) (f[i])
#define int long long
using namespace std;
const int MAXN = 5e4 + 10;
int n;
struct Node{
	int w, h;
} a[MAXN];
int f[MAXN];
bool cmp(Node i, Node j) {
	return (i.h > j.h) || (i.h == j.h && i.w > j.w);
}
double slope(int i, int j) {
	return (Y(j) - Y(i)) / (double)(X(j) - X(i));
}
int head, tail, q[MAXN];
signed main() {
	scanf("%lld", &n);
	for(int i = 1; i <= n; i++) {
		scanf("%lld%lld", &a[i].w, &a[i].h);
	}
	sort(a + 1, a + n + 1, cmp);
	int t = 0;
	for(int i = 1; i <= n; i++) {
		if(a[i].w > a[t].w) a[++t] = a[i];
	}
	n = t;
	head = tail = 1;
	for(int i = 1; i <= n; i++) {
		while(head < tail && slope(q[head], q[head + 1]) <= a[i].w) {
			head++;
		}
		int j = q[head]; f[i] = f[j] + a[i].w * a[j + 1].h;
		while(head < tail && slope(q[tail - 1], q[tail]) >= slope(q[tail], i)) {
			tail--;
		}
		q[++tail] = i;
	}
	cout << f[n] << endl;
	return 0;
}

总结？#

如果转移方程能表示成： $f_i=\max_{j<i}{\{a_ib_j+c_j+d_i\}}$ 的形式（或 $\min$ ），并且 $a_i$ 关于 $i$ 有单调性，就都可以用斜率优化。

斜率优化能把 $\mathcal{O}(n^2)$ 降成 $\mathcal{O}(n)$ .

数形结合。

代码短。