【CodeForces-1495A】Diamond Miner • TonyYin's Blog

题意#

给定 $2n$ 个点，其中 $n$ 个在 $x$ 轴上，另外 $n$ 个在 $y$ 轴上。现在要求每一个 $x$ 轴上的点与一个 $y$ 轴上的点连线，每个点恰好被连线一次。求所有线段的欧几里得距离之和。

分析#

首先根据数据范围 $n\leq 10^5$ ，在考场可以判断出贪心或二分。

之后看到样例解释的配图，发现可以抽象出：对于两条线段的模型。

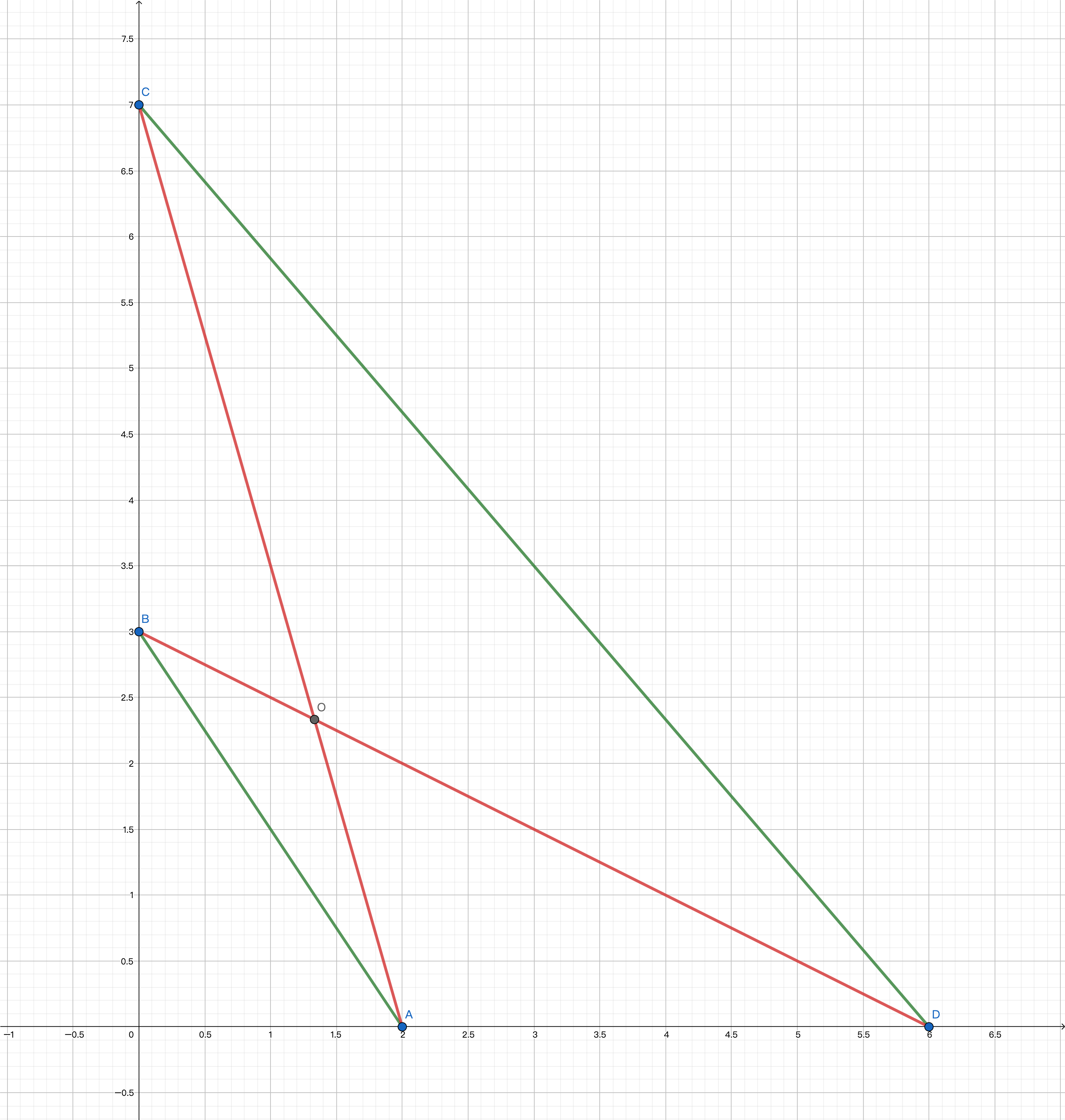
由上图可以看出，对于四个点，只有两种连线方法：不交叉或交叉。

不交叉的欧几里得距离和为： $|AB|+|CD|$ ，交叉的欧几里得距离为 $|AC|+|BD|$ .

经过肉眼观测，我们可以用小学数学证明不交叉一定优于交叉：

由于三角形任意两边之和大于第三边，所以 $|AB|<|AO|+|BO|$ ， $|CD|<|CO|+|DO|$ .

于是 $|AB|+|CD|<|AO|+|BO|+|CO|+|DO|=|AC|+|BD|$ .

将结论推广到 $n$ 条线段，发现所有线段都不交叉是最优的，否则将交叉的两个线段交换，可以使距离和更小。

考虑如何按照这个方法，对所有点进行两两配对。

容易想到，把所有处于负半轴上的点，对称到正半轴上。这样处理后距离和不变。

所以，把 $x$ 轴上的点和 $y$ 轴上的点分别按照横竖坐标升序排序，排名相同的点进行配对，一定不会交叉。

代码#

~~考场代码~~

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 1e5 + 10;
int T;
double a[MAXN], b[MAXN];
signed main() {
    cin >> T;
    while(T--) {
        int n, cnt1 = 0, cnt2 = 0; cin >> n;
        for(int i = 1; i <= 2 * n; i++) {
            int x, y; scanf("%lld%lld", &x, &y);
            if(x == 0) {
                if(y < 0) y *= -1;
                a[++cnt1] = y;
            }
            if(y == 0) {
                if(x < 0) x *= -1;
                b[++cnt2] = x;
            }
        }
        sort(a + 1, a + n + 1); sort(b + 1, b + n + 1);
        double ans = 0;
        for(int i = 1; i <= n; i++) {
            ans += sqrt(a[i] * a[i] + b[i] * b[i]);
        }
        printf("%.11lf\n", ans);
    }
    return 0;
}

cpp