【洛谷-P2900】Land Acquisition

题目描述#

翻译的不是很好，所以我简化一下题面。

给定 $n$ 个矩阵的宽 $w$ 和高 $h$，每次选一个矩阵集合，代价为集合中的 $\max{\{w\}}\times \max{\{h\}}$。

任意两次之间没有重复的矩阵，求取完所有矩阵的最小代价。

定义#

矩阵的两个参数为 $w, h$，分别对应下图中的宽和高。

函数 $\operatorname{slope}(i, j)$ 表示 $(x_i, y_i)$ 与 $(x_j, y_j)$ 构成的直线的斜率，$x, y$ 的含义在下面会说。

分析#

注意到对于两个矩阵 $i, j$，如果 $w_i\leq w_j$ 并且 $h_i\leq h_j$，那么 $i$ 和 $j$ 一定可以放到一组，$i$ 对答案没有贡献，不用考虑，可以直接删去。

比如下图当中的 $1$ 和 $2$. 矩阵 $2$ 能完全被 $1$ 包含，所以 $2$ 没有贡献，可以删去。

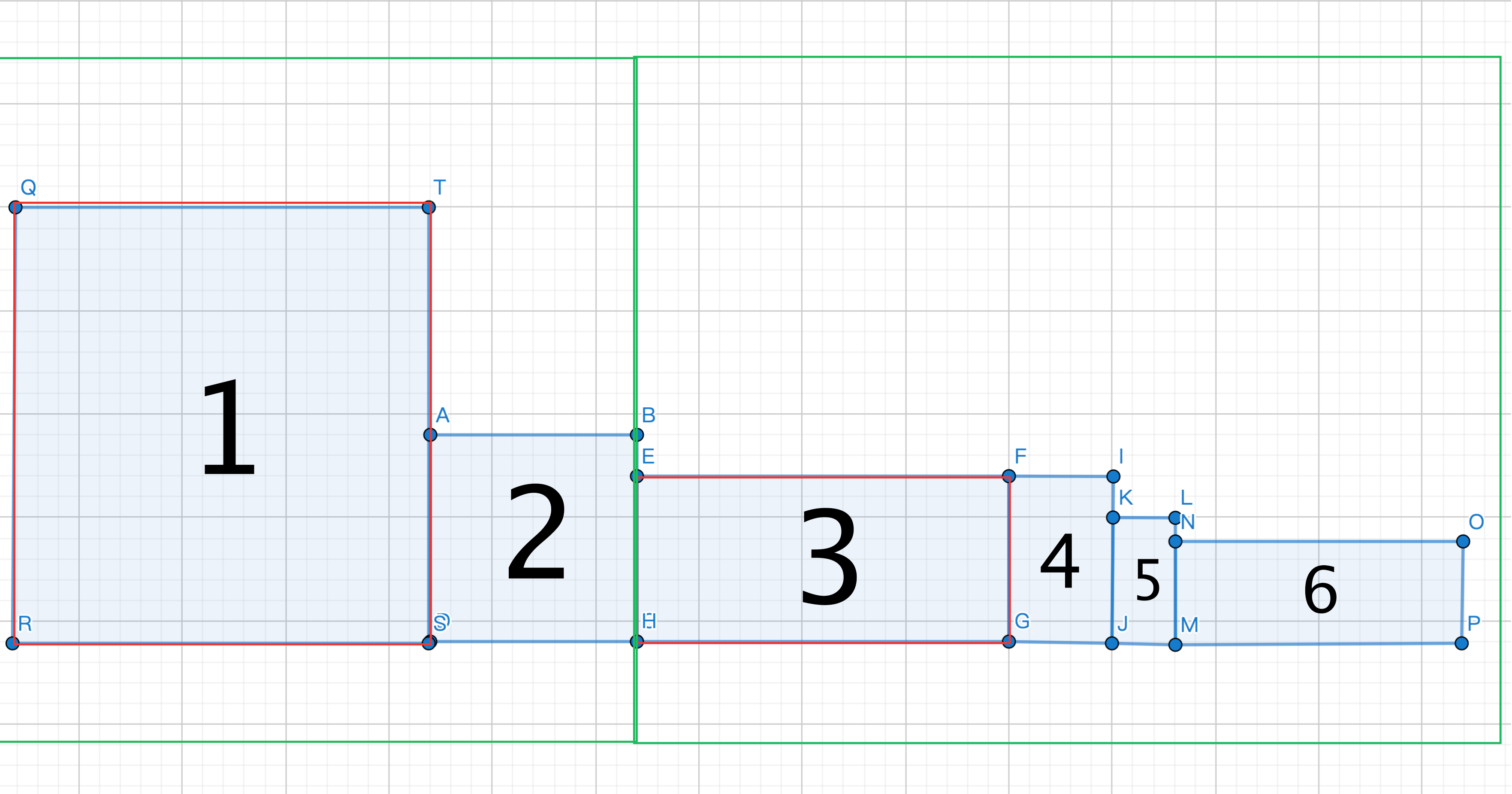
于是考虑先删除所有 $i$ 这样的矩阵。

具体做法就是：按照 $h$ 为第一关键字，$w$ 为第二关键字从大到小排序，之后双指针扫一遍即可。

//a已经降序排序
int t = 0;
for(int i = 1; i <= n; i++) {
	if(a[i].w > a[t].w) a[++t] = a[i];
}

如上图，剩下的只有 $1, 3$ 号矩阵。

删完之后剩下的就是一个，$h$ 严格单调递减，$w$ 严格单调递增的序列。考虑 $DP$ 解决。

DP#

设 $f_i$ 为新序列中，取走前 $i$ 个矩阵的最小花费，$w$ 为宽（单调递增），$h$ 为高（单调递减），那么有转移方程：

相当于，把 $j+1$ 到 $i$ 这一段合为一组取走。由于单调性，所以这一组的 $\max{\{w\}}=w_i$，$\max{\{h\}}=h_{j+1}$.

复杂度 $\mathcal{O}(n^2)$。这显然可以斜率优化。

斜率优化#

我们目前优化的目的，是尽快地找到 $f_i$ 到底是由哪个 $j$ 转移过来的，也就是尽快找到最小化 $f_i$ 的继承状态。

为了表示方便，设 $j$ 为能使 $f_i$ 最小化的继承状态，所以有：

考虑一次函数斜截式 $y=kx+b$ 或 $b=y-kx$，将状态转移方程变换为这个形式：

其中变量 $x, y$ 与 $j$ 有关，$b, k$ 与 $j$ 无关。且要求 $x$ 随 $j$ 单调递增，$b$ 中包含 $f_i$（斜率优化基本操作）。

所以可以构造出直线方程为：

我们把 $(x, y)$ 看成平面直角坐标系上的点。那么现在 $(x_j, y_j)$ 的意义就是：直线 $y=kx+b$ 上的一个点。

又因为我们的目的是最小化 $f_i$，在上面的表示当中，$f_i$ 只与直线的截距 $b$ 有关。所以显然地，问题转化为：如何选取 $j$ ，才能使得过点 $(x_j, y_j)$ 的直线的截距 $b$ 最小。

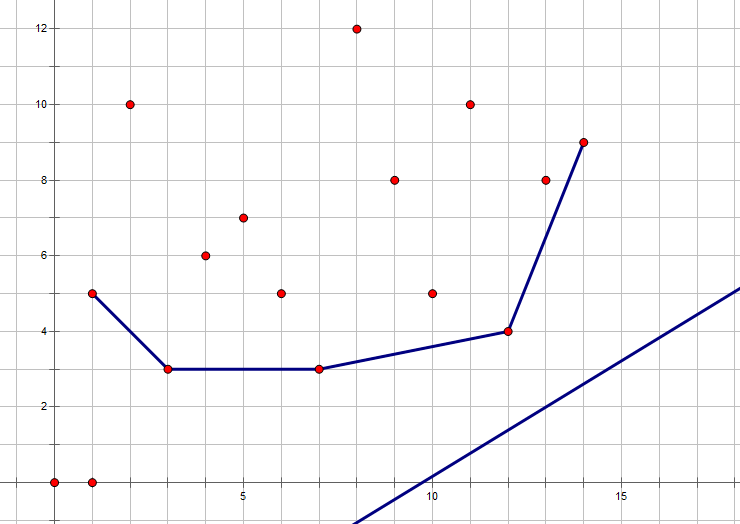
显然，对于一个斜率 $k$ 来说，最优解 $j$ 就是从左往右枚举到的第一个 $\operatorname{slope}(j, j+1)>k$ 的点。（其中 $\operatorname{slope}$ 的定义在上面有说过）

再考虑单调性： $x$ 随 $j$ 单调递增，$k$ 随 $i$ 单调递增，要使截距 $b=f_i$ 最小。

显然，所有的最优决策点 $j$ 都在下凸包上，也就是上图中的折线。

所以单调队列维护下凸包即可：

设单调队列（递增）为 $q$，队首为 $head$，队尾为 $tail$，当前要转移 $i$ 号点，那么具体步骤：

1. 当 $\operatorname{slope}(q_{head}, q_{head+1})\leq w_i=k_i$ 时，$head$++，（保证最优解）
2. 此时的 $q_{head}$ 就是最优转移点，根据它和转移方程计算出 $f_i$，
3. 当 $\operatorname{slope}(q_{tail-1}, q_{tail})\geq\operatorname{slope}(q_{tail}, i)$ 时，$tail$—，（维护下凸包）
4. 在队尾插入 $i$.

代码#

#include <bits/stdc++.h>
#define X(i) (-a[i+1].h)
#define Y(i) (f[i])
#define int long long
using namespace std;
const int MAXN = 5e4 + 10;
int n;
struct Node{
	int w, h;
} a[MAXN];
int f[MAXN];
bool cmp(Node i, Node j) {
	return (i.h > j.h) || (i.h == j.h && i.w > j.w);
}
double slope(int i, int j) {
	return (Y(j) - Y(i)) / (double)(X(j) - X(i));
}
int head, tail, q[MAXN];
signed main() {
	scanf("%lld", &n);
	for(int i = 1; i <= n; i++) {
		scanf("%lld%lld", &a[i].w, &a[i].h);
	}
	sort(a + 1, a + n + 1, cmp);
	int t = 0;
	for(int i = 1; i <= n; i++) {
		if(a[i].w > a[t].w) a[++t] = a[i];
	}
	n = t;
	head = tail = 1;
	for(int i = 1; i <= n; i++) {
		while(head < tail && slope(q[head], q[head + 1]) <= a[i].w) {
			head++;
		}
		int j = q[head]; f[i] = f[j] + a[i].w * a[j + 1].h;
		while(head < tail && slope(q[tail - 1], q[tail]) >= slope(q[tail], i)) {
			tail--;
		}
		q[++tail] = i;
	}
	cout << f[n] << endl;
	return 0;
}