【APIO2010】特别行动队

题意#

给定一个长度为 $n$ 的序列，每个元素有权值 $x_i$，现在要将序列分割为若干段，每段中元素连续。设 $s_i$ 表示前缀和，即 $s_i=\sum_{j=1}^{i}{x_j}$，那么对于每段 $[l, r]$，代价为：

其中 $a, b, c$ 为题目给定的常数。整个序列的代价为每段代价之和。

求序列的代价最大值。

$1\leq n\leq 10^6, -{10}^7\leq b, c\leq 10^7, 1\leq x_i\leq 100$.

注意：$-5\leq \textcolor{red}{a} \leq -1\textcolor{red}{<0}$.

DP#

容易想到时间复杂度为 $\mathcal{O}(n^2)$ 的 DP 做法。

令 $f_i$ 为前 $i$ 个物品，分若干段的最小代价，有状态转移方程：

其中 $s_i$ 与题目中定义相同，为 $x$ 的前缀和。

但发现 $1\leq n\leq 10^6$，所以这样的 DP 无法通过此题，考虑如何优化。

优化#

发现对于 $f_i$ 来说，一定存在唯一的 $j<i$ 对 $f_i$ 进行了更新，使得 $f_i$ 取到最大值。所以不妨设 $j$ 为能使 $f_i$ 最大化的继承状态， 那么对暴力的状态转移方程进行整理：

（这就很斜率优化

考虑一次函数的斜截式 $y=kx+b$，将方程转化为这个形式。其中变量 $x, y$ 与 $j$ 有关，$b, k$ 与 $j$ 无关，且要求 $x$ 随 $j$ 单调递增。

那么：

所以：

观察 $b$ 这一项。要最大化 $f_i$，而 $-b\cdot s_i-a\cdot{s_i}^2$ 为常数，所以只要最大化 $b$ 即可。

由于 $x, y$ 只与 $j$ 有关，不妨设 $(x_j, y_j)$ 为平面直角坐标系上的一些点。那么问题就转化为，如何选取 $j$，才能使得，斜率固定为 $k$ 的，且过点 $(x_j, y_j)$ 的直线的截距 $b$ 最大。

（斜率为定值 $k$，是因为 $2a\cdot s_i$ 也都是题目给定的定值。

那么问题转化到了平面上。

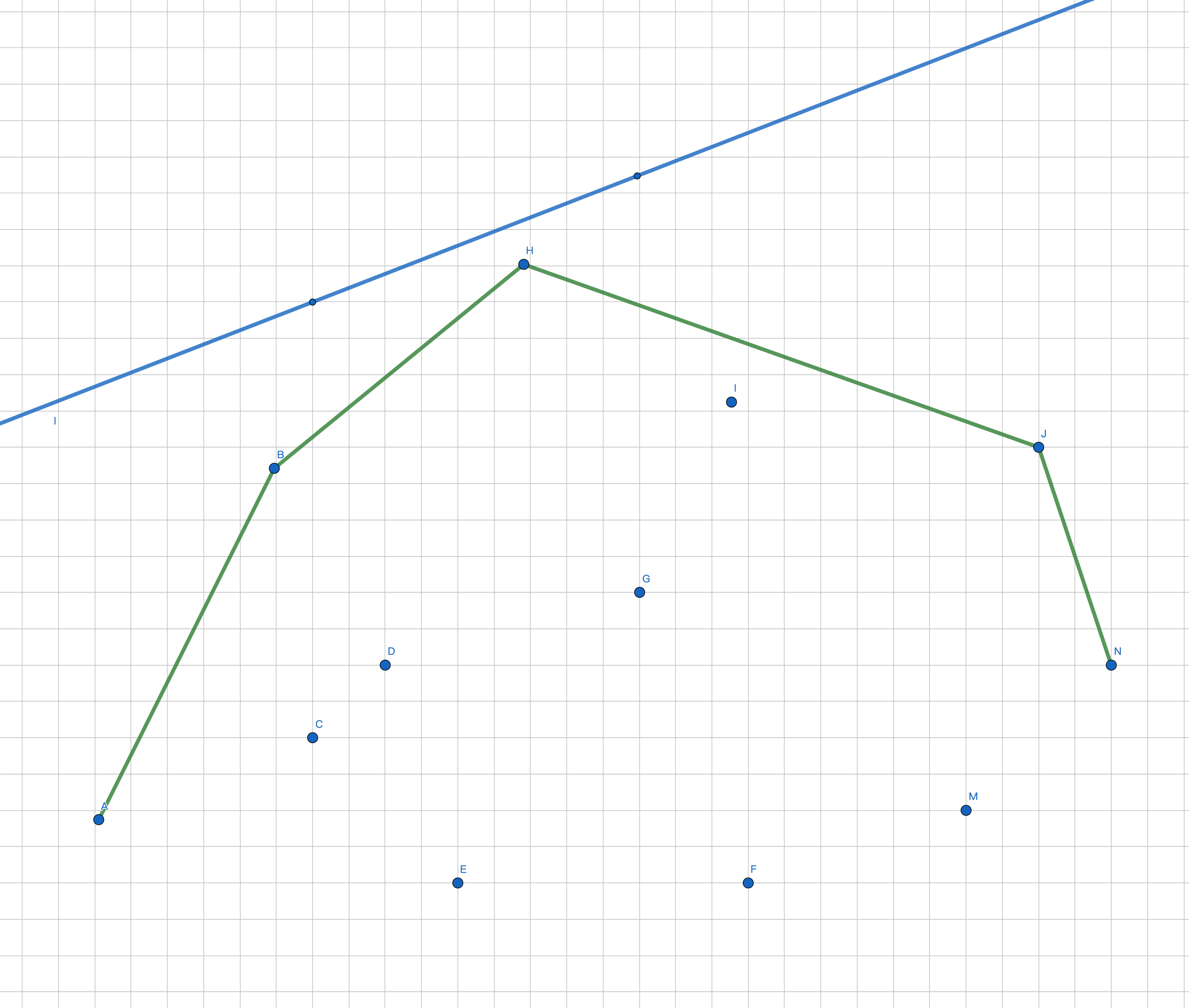
由上图可以形象的看出，使直线截距最大的点（最优决策点），就是将直线向下平移时第一个碰到的点。

而且显然对于任意的斜率 $k$ 来说，最优决策点只有可能在上凸包上，也就是上图中，绿色直线所覆盖的点。

继续观察，在上图中可以看出，对于斜率为 $k$ 的直线，最优解 $j$ 就是第一个 $\operatorname{slope}(j, j+1)<k$ 的点。（$\operatorname{slope}(a, b)$ 表示 $(x_a, y_a), (x_b, y_b)$ 两点构成直线的斜率）

又因为本题中，$k$ 随 $i$ 递增而递减，与上凸包单调性相同，所以考虑使用单调队列解决。

单调队列#

设单调队列（递增）为 $q$，队首为 $head$，队尾为 $tail$，当前要转移 $i$ 号点，具体步骤：

1. 当 $\operatorname{slope}(q_{head}, q_{head+1})\textcolor{red}{\geq}2a\cdot s_i$ 时，$head$++，（保证最优解）

2. 此时的 $q_{head}$ 就是最优转移点，根据它和转移方程计算出 $f_i$，

3. 当 $\operatorname{slope}(q_{tail-1}, q_{tail})\textcolor{red}{\leq}\operatorname{slope}(q_{tail}, i)$ 时，$tail$—，（维护上凸包）

4. 在队尾插入 $i$.

代码#

注意多组数据即可。

#include <bits/stdc++.h>
#define int long long
#define x(X) (s[X])
#define y(X) (f[X] + a * s[X] * s[X] - b * s[X] + c)
using namespace std;
const int MAXN = 1e6 + 10;
int n;
int a, b, c;
int s[MAXN], f[MAXN];
int head, tail, q[MAXN];
double slope(int i, int j) {
	return 1.0 * (y(j) - y(i)) / (x(j) - x(i));
}
signed main() {
	int T; scanf("%lld", &T);
	while(T--) {
		scanf("%lld%lld%lld%lld", &n, &a, &b, &c);
		for(int i = 1; i <= n; i++) {
			int tmp; scanf("%lld", &tmp);
			s[i] = s[i - 1] + tmp;
		}
		head = tail = 1;
		for(int i = 1; i <= n; i++) {
			while(head < tail && slope(q[head], q[head + 1]) >= 2ll * a * s[i])
                head++;
			int j = q[head];
            f[i] = f[j] + a * (s[i]-s[j])*(s[i]-s[j]) + b*(s[i]-s[j]) + c;
			while(head < tail && slope(q[tail - 1], q[tail]) <= slope(q[tail], i))
                tail--;
			q[++tail] = i;
		}
		cout << f[n] << endl;
	}
	return 0;
}