DP专题分享
宝藏
状压DP。
位运算技巧
| 位运算 | 功能 | 示例 |
|---|---|---|
| $\texttt{x>>k}$ | 去掉最后 $k$ 位 | $101101\rightarrow 101, k=3$ |
| $\texttt{x<<k}$ | 在最后加 $k$ 个 $0$ | $101101\rightarrow 101101000, k=3$ |
| $\texttt{x<<1|1}$ | 在最后加一个 $1$ | $101101\rightarrow 1011011$ |
| $\texttt{x|1}$ | 把第 $1$ 位变成 $1$ | $101100\rightarrow 101101$ |
| $\texttt{x|(1<<(k-1))}$ | 把第 $k$ 位变成 $1$ | $101001\rightarrow 101101, k=3$ |
| $\texttt{x|((1<<k)-1)}$ | 把末 $k$ 位变成 $1$ | $101001\rightarrow 101111, k=4$ |
| $\texttt{x&(-2)}$ | 把第 $1$ 位变成 $0$ | $1010111\rightarrow 1010110$ |
| $\texttt{x & (~(1<<(k-1)))}$ | 把第 $k$ 位变成 $0$ | $1010110\rightarrow 1000110, k=5$ |
| $\texttt{x&(-(1<<k))}$ | 把末 $k$ 位变成 $0$ | $1010110\rightarrow 1000000, k=5$ |
| $\texttt{x ^ 1} $ | 把第 $1$ 位取反 | $101101\rightarrow 101100$ |
| $\texttt{x ^ (1<<(k-1))}$ | 把第 $k$ 位取反 | $101001\rightarrow 101101, k=3$ |
| $\texttt{x ^ ((1<<k)-1)}$ | 把末 $k$ 位取反 | $1101101\rightarrow 1100010, k=4$ |
| $\texttt{x&7}$ | 取末 $3$ 位 | $1101101\rightarrow 101$ |
| $\texttt{x&(1<<(k-1))}$ | 取末 $k$ 位 | $1101101\rightarrow 01101, k=3$ |
| $\texttt{(x>>(k-1))&1}$ | 取第 $k$ 位 | $1101101\rightarrow 1, k=4$ |
| $\texttt{x&(x+1)}$ | 把末尾连续的 $1$ 变成 $0$ | $100101111\rightarrow 100100000$ |
| $\texttt{x|(x+1)}$ | 把右边第一个 $0$ 变成 $1$ | $100101111\rightarrow 100111111$ |
| $\texttt{x|(x-1)}$ | 把末尾连续的 $0$ 变成 $1$ | $100101000\rightarrow 100101111$ |
| $\texttt{(x ^ (x+1))>>1}$ | 取末尾连续的 $1$ | $100101111\rightarrow 1111$ |
| $\texttt{x&(-x)}$ | 取右边第一个 $1$ 及其右侧 | $100101000\rightarrow 1000$ |
枚举子集、子集的子集
枚举子集
用 $T$ 表示 $S$ 的子集,则一种枚举子集的方式是:
\begin{array}{ll}
1& \textbf{for }( \textbf{int } \text{T = S; T; T=(T – 1) & S)}\\
2& \qquad \text{Do Something (T is a nonempty subset of S)}
\end{array}
$$
单次枚举 $T$ 的复杂度是 $\mathcal{O}(2^{|S|})$ 的。
枚举子集的子集
若要枚举 $S$ 的所有子集的子集,可以证明复杂度为 $\mathcal{O}(3^n)$.
组合意义天地灭,代数推导保平安。
复杂度为:
\begin{aligned}
\sum_{T\subseteq S}2^{|T|}=\sum_{i=1}^n\binom{n}{i} 2^i&=\sum_{i=1}^n\binom{n}{i}2^i1^{n-i}\\
&=(1+2)^n-1\Rightarrow \mathcal{O}(3^n)
\end{aligned}
$$
证毕,参考 枚举子集为什么是 O(3^n) 的 – Jijidawang – 博客园。
题意
参与考古挖掘的小明得到了一份藏宝图,藏宝图上标出了 $n$ 个深埋在地下的宝藏屋, 也给出了这 $n$ 个宝藏屋之间可供开发的 $m$ 条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是,每个宝藏屋距离地面都很远,也就是说,从地面打通一条到某个宝藏屋的道路是很困难的,而开发宝藏屋之间的道路则相对容易很多。
小明的决心感动了考古挖掘的赞助商,赞助商决定免费赞助他打通一条从地面到某个宝藏屋的通道,通往哪个宝藏屋则由小明来决定。
在此基础上,小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路,小明就会与考古队一起挖掘出由该条道路所能到达的宝藏屋的宝藏。另外,小明不想开发无用道路,即两个已经被挖掘过的宝藏屋之间的道路无需再开发。
新开发一条道路的代价是 $\mathrm{L} \times \mathrm{K}$。其中 $L$ 代表这条道路的长度,$K$ 代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的宝藏屋的数量(包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋) 。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路,使得工程总代价最小,并输出这个最小值。
对于 $ 100\%$ 的数据: $1 \le n \le 12$,$0 \le m \le 10^3$,$v \le 5\times 10^5$。
题解
找个生成树,代价和最小。
设 $f_{S, i}$ 表示当前包含的点集是 $S$,树高是 $i$,此时的最小代价和。
则:
f_{S, i}=\min_{T\subseteq S} \{f_{T, i-1}+w(T, S)\}
$$
其中 $w(T, S)$ 代表从 $T$ 变到 $S$ 的代价,预处理。
预处理时,先找新增加的点,再找从 $T$ 连到这个点的最小边权,求和即可。顺便判断不合法的 $(T, S)$ 组合。
垃圾陷阱
题意
给定深井的深度 $D$ 和垃圾的数量 $G$.
XLL想把垃圾堆起来,等到堆得与井同样高时,她就能逃出井外了。
XLL可以通过吃垃圾来维持自己的生命。
每个垃圾都可以用来吃或堆放,并且堆放垃圾不用花费XLL的时间。
给定每个垃圾扔下的时间 $t_i$,高度 $h_i$,可供维持 $f_i$ 小时的生命。
XLL在 $0$ 时刻位于井底,要保证任何时刻的生命储备时长(生命值) $>0$,初始时生命值为 $10$ 小时。
求最早何时爬出,或最长存活多久。
$2\leq D,G\leq 100$,$1\leq t\leq 1000$,$1\leq h\leq 25$,$1\leq f \leq 30$.
分析
背包。
井 $\Rightarrow$ 背包大小,垃圾高度 $\Rightarrow$ 物品重量,维持生命的时长 $\Rightarrow$ 价值。
对物品按 $t_i$ 升序排序,顺序加入背包。
设 $g[i][j]$ 表示处理完前 $i$ 件物品后,高度为 $j$ 时的最大生命值,有转移:
g_{i, j} = \max\left\{\begin{array}{l}g_{i – 1, j} + f[i]\\g_{i-1, j-h[i]}\end{array}\right.
$$
普通的 $0/1$ 背包即可解决。
[BJOI2019]排兵布阵
题意
一个游戏,有 $n$ 座城堡,每局对战有两名玩家,每名玩家有 $m$ 个士兵,每人可以向第 $i$ 个城堡派遣 $a_i$ 名士兵,士兵总数满足:$a_1+a_2+\cdots+a_n\leq m$.
二人争夺这些城堡,如果一名玩家向城堡 $i$ 派遣的士兵数严格大于对手士兵数的两倍,那么这名玩家占领了这座城堡,获得 $i$ 分。
现给定 $s$ 名玩家及其各自的派兵策略,你需要选定一个固定的派兵策略,最大化你在 $s$ 场游戏中的总得分。
$1\leq s\leq 100, 1\leq n\leq 100, 1\leq m\leq 20000$.
分析
设 $f_{i,j}$ 表示:对于前 $i$ 个城堡共派出 $j$ 个士兵;设 $a_{i,j}$ 表示:在城堡 $i$,玩家 $j$ 的出兵数量。
对每个城堡,把各个玩家在该城堡的出兵数量,按升序排序。
这样一来,若你在城堡 $i$ 的出兵数量大于 $2\times a_{i,j}$,则你可以在城堡 $i$ 获得 $i\times j$ 的得分。
于是对每个赢得城堡 $i$,枚举要战胜前 $k$ 个玩家,分别转移即可:
f[i][j]=\max_{k=1}^s
\left\{
\begin{array}{lr}
0, &j-a_{i,k}\times 2 – 1 < 0\\
f[i][j-a_{i, k}\times2-1]+k\cdot i, &j-a_{i,k}\times2-1\geq 0
\end{array}
\right.
$$
属于分组背包模型。
代码
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 108, MAXM = 20008, MAXS = 108;
int s, n, m;
int dp[MAXM], a[MAXN][MAXS];//a[i][j]表示第i个城堡,第j个玩家
int main() {
scanf("%d%d%d", &s, &n, &m);
for(int i = 1; i <= s; i++)
for(int j = 1; j <= n; j++)
scanf("%d", &a[j][i]);
for(int i = 1; i <= n; i++)
sort(a[i] + 1, a[i] + s + 1);
for(int k = 1; k <= n; k++) {
for(int i = m; i > 0; i--) {
for(int j = 1; j <= s; j++) {
if(i >= a[k][j] * 2 + 1) {
dp[i] = max(dp[i], dp[i - a[k][j] * 2 - 1] + k * j);
}
}
}
}
cout << dp[m] << endl;
return 0;
}
[BOI2003]Gem 气垫车
题意
给出一棵 $N$ 个点的树,要求你为树上的结点标上权值,权值可以是任意的正整数。
唯一的限制条件是相邻的两个结点不能标上相同的权值。
求一种方案,使得整棵树的总价值最小,只需要输出最小价值。
$1\leq N\leq 10000$.
分析
结论:用 $\log n$ 种颜色即可。于是树上背包,容易通过。
[USACO12FEB]Nearby Cows G
题意
给定一棵 $n$ 个点的数,点带权。对于每个节点 $i$,求出距离 $i$ 不超过 $k$ 的所有节点的权值和。
$1\leq n\leq 10^5$,$1\leq k\leq 20$,$0\leq c_i\leq 1000$.
分析
考虑树形DP。
先任意钦定 $\rm{root}$.
设 $f_{i, j}$ 表示在 $i$ 的子树中,距离 $i$ 小于等于 $j$ 的节点的权值和。
可以用一次 $\rm {DFS}$ 求得 $f$,转移如下:
f_{x, i}=c_x+\sum_{v} f_{v, i-1}
$$
设 $g_{i, j}$ 表示所有距离 $i$ 距离小于等于 $j$ 的节点的权值和,所以 $\operatorname{Ans}_i = g_{i,k}$.
再用一次 $\rm{DFS}$ 求得 $g$,转移如下:
g_{x,i} = \left\{\begin{array}{lr}
f_{x, i}+\sum\limits_{v}(g[\operatorname{fa}][i-1]-f_{x, i-2}), &x=1\\
f_{x, i}, &x\neq 1
\end{array}\right.
$$
注意当 $i=1$ 时,应忽略 $f_{x, i-2}$ 项,否则会数组越界。
代码
const int MAXN = 1e5 + 10, MAXK = 25;
int n, k, c[MAXN];
vector<int> g[MAXN];
int f[MAXN][MAXK];
void dfs1(int x, int fa) {
for(int i = 0; i <= k; i++) f[x][i] = c[x];
for(int v : g[x]) {
if(v == fa) continue;
dfs1(v, x);
for(int i = 1; i <= k; i++) f[x][i] += f[v][i - 1];
}
}
void dfs2(int x, int fa) {
if(x != 1) {
for(int i = k; i >= 2; i--)
f[x][i] += f[fa][i - 1] - f[x][i - 2];
f[x][1] += f[fa][0];
}
for(int v : g[x]) {
if(v == fa) continue;
dfs2(v, x);
}
}
int main() {
n = read(), k = read();
for(int i = 1; i < n; i++) {
int u = read(), v = read();
g[u].push_back(v), g[v].push_back(u);
}
for(int i = 1; i <= n; i++) c[i] = read();
dfs1(1, 0); dfs2(1, 0);
for(int i = 1; i <= n; i++) cout << f[i][k] << "\n";
return 0;
}
Coloring Brackets
题意
给定一个合法括号序列,对序列按照如下方法染色:
- 每个括号的颜色:红色、蓝色、或不染色;
- 每对匹配的括号:有且仅有其中一个被染色;
- 相邻两个括号:若都有颜色,要求它们的颜色互不相同。
求符合条件的染色方案数,对 $10^9+7$ 取模。
序列长度:$2\leq |s|\leq 700$.
分析
将颜色映射到三个数:
\operatorname{Color}=\left\{\begin{array}{ll}
0 & \text{No Color}\\
1 & \text{Red}\\
2 & \text{Blue}\\
\end{array}\right.
$$
设 $f[l][r][x][y]$ 为区间 $[l, r]$ 内,且 $\operatorname{Color}_l=x, \operatorname{Color}_r=y$ 的方案数。
下面分类讨论状态转移方式:
情况一:$()$
若 $l+1=r$,则这段序列仅有一对左右括号,只能对其中一个染色。
作为初始情况,可直接赋值:
f[l][r][0][1]=f[l][r][0][2]=f[l][r][1][0]=f[l][r][2][0]=1
$$
情况二:$(\dots\dots)$
若 $l$ 与 $r$ 配成一对括号,则枚举 $\operatorname{Color}_{l+1}$ 和 $\operatorname{Color}_{r-1}$,从 $f[l+1][r-1]$ 进行转移。
f[l][r][x][y]=\sum_{i=0\vee i\neq x}\,\sum_{j=0\vee j\neq y} f[l+1][r-1][i][j]
$$
情况三:$(\dots\dots) \dots(\dots)$
要求 $l$ 是左括号,$r$ 是右括号。设 $\operatorname{R}[i]$ 表示与 $i$ 配对的右括号。
用 $f[l][\operatorname{R}[l]]\times f[\operatorname{R[l]+1}][r]$ 进行转移,具体过程要枚举四个颜色,就不做形式化表达了。
for(int i = 0; i <= 2; i++) {
for(int j = 0; j <= 2; j++) {
for(int p = 0; p <= 2; p++) {
for(int q = 0; q <= 2; q++) {
if((j == 1 && p == 1) || (j == 2 && p == 2)) continue;
(f[l][r][i][q] += (f[l][R[l]][i][j] * f[R[l] + 1][r][p][q]) % mod) %= mod;
}
}
}
}
[POI2010]ZAB-Frog
题意
数轴上有 $n$ 个点,坐标分别为 $p_1, p_2, \cdots, p_n$ 在这些点上按照某些规则跳。
规则是:每次向距当前点第 $k$ 小的点跳,如果有相同距离则向下标较小的跳;
求从每个点出发跳了 $m$ 次后在哪里.
$1\leq k < n\leq 10^6, 1\leq m\leq 10^{18}, 1\leq p_i\leq 10^{18}$.
$\rm{Part}$ $\rm{1}$
首先,注意到 $k$ 是固定的,所以可以先预处理,对于每个点 $i$,跳一次之后的位置$\operatorname{next}_i$.
这部分使用单调队列处理。
我们知道,对于每个点,距离其前 $k$ 小的点分布在其两侧,可以用一段完整区间覆盖。
所以我们想到,当单调队列枚举到 $i$ 时,单调队列中维护的区间,就是覆盖距离 $i$ 前 $k$ 小的点的区间。这样找到区间内距离最大的点就是我们要求的 $\operatorname{next}_i$,下面考虑考虑如何维护。
对于区间 $[l, r]$ 中的一个点 $i$,距离他最远的点一定是 $l$ 和 $r$ 这两个点中的一个。如果 $r+1$ 到 $i$ 的距离小于了 $l$ 到 $i$ 的距离,说明区间应当向右滑动,如下图,$n=7, k=3$ 的例子:
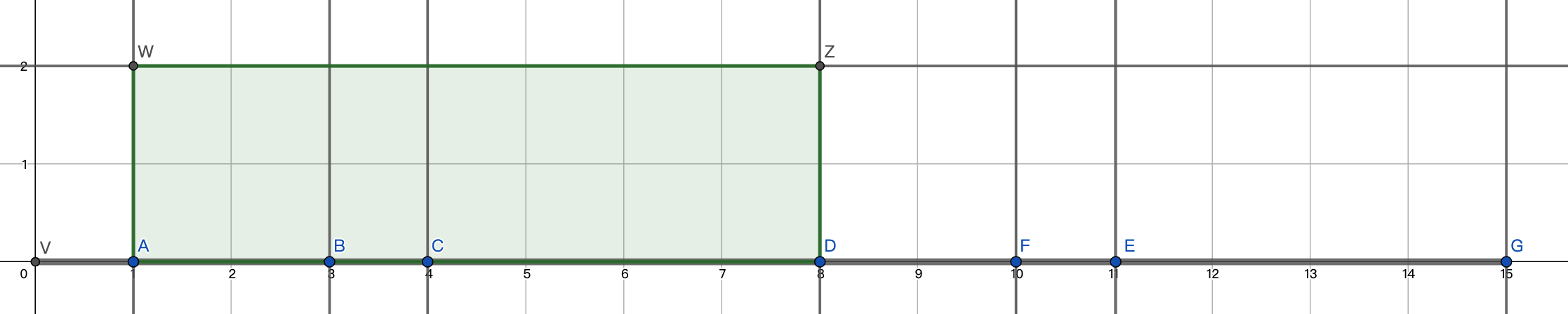
绿色区间是距离点 $C$ 前 $k$ 小的点,考虑距离点 $D$ 前 $k$ 小的点。
$\text{Dis(D, F) < dis(d, a)}$,所以区间要右移一个单位,变成:

又因为 $\text{Dis(D, E) < dis(d, b)}$,所以区间要再右移一个单位,变成:

至此,我们能够求出每个点,距离其第 $k$ 小的点的下标。
head = 1, tail = k + 1;
for(int i = 1; i <= n; i++) {
while(tail + 1 <= n && x[tail + 1] - x[i] < x[i] - x[head]) head++, tail++;
if(x[tail] - x[i] > x[i] - x[head]) nxt[i] = tail;
else nxt[i] = head;
}
$\rm{Part}$ $\rm{2}$
题目要求跳 $m$ 次之后的答案,我们使用类似快速幂的方法,倍增处理即可。
for(int i = 1; i <= n; i++) pos[i] = i;
while(m) {
if(m & 1) {
for(int i = 1; i <= n; i++) pos[i] = next[pos[i]];
}
m >>= 1;
for(int i = 1; i <= n; i++) next2[i] = next[i];
for(int i = 1; i <= n; i++) next[i] = next2[next2[i]];
}
代码
最终代码在上面两部分的基础上加上 $\rm{I/O}$ 即可。
Good Contest
题意
数列 $a$ 在下列条件下随机生成。
$a_i$ 是给定的区间 $[l_i, r_i]$ 内的正整数,等概率随机。
求 $a_{1\cdots n}$ 单调不增的概率,对 $998244353$ 取模。
$2\leq n\leq 50$,$0\leq l_i, r_i\leq 998244351$.
分析
A=\prod_{i=1}^n (r_i-l_i+1)
$$
只需求出单调不增的序列个数 $B$,则:
p=\frac{B}{A}\bmod 998244353
$$
对于值域较小的情况,可以想到设 $f_{i,j}$ 表示:选好了前 $i$ 个数且 $a_i=j$ 的情况下的方案数。
转移只需:
f_{i,j}=\sum_{k\geq j} f_{i-1, k}
$$
但可惜本题中值域较大,考虑做优化。
想到离散化。
对区间端点进行离散化,用 $p_i$ 表示所有端点坐标中数值第 $i$ 大的数,
$a_i$ 表示左端点离散化后编号,$b_i$ 表示右端点离散化后编号。
此时需要微调DP状态,但思路类似。
设 $f_{i, j}$ 表示选好了前 $i$ 个数且 $a_i\in [p_j, p_{j+1}-1]$,所形成单调不增数列的方案数。
转移时,由于进行了离散化,我们无法通过枚举确定 $a_{i-1}$ 与 $a_i$ 的大小关系。
退而求其次,再枚举 $k$,保证 $a_{k+1},\cdots,a_i$ 的值都在 $[p_j, p_{j+1}-1]$ 内,计算这个长度为 $k$ 的区间内的方案数。
记可能的取值个数 $L = p_{j+1}-p_j$.
需要在其中选 $i-k$ 个数单调不增,方案数为:
C_{i-k}=\binom{L+i-k-1}{i-k}
$$
这个组合数直接递推预处理就好了:
C_x=\binom{L+x-1}{x}
\left\{\begin{array}{lr}
L, &x=1
\\
C_{x-1}\cdot (L+x-1)\cdot \operatorname{Inv}(x), &x>1
\end{array}\right.
$$
转移时,倒序枚举所有合法的 $k$,具体地:
f_{i,j}=\sum_{j\in [a_k, b_k]\wedge k < i}(f_{k, j+1}\cdot C_{i-k})
$$
每个 $i$ 转移完之后,需要做前缀和,
f_{i,j}=\sum_{k\geq j} f_{i, k}
$$
这样对下一次转移才是对的。
最终 $B=f_{n, 1}$,答案为:
\operatorname{Ans}=\frac{B}{A} \bmod 998244353
$$
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN = 60, mod = 998244353;
inline int power(int x, int k) {
int ret = 1;
while(k) {
if(k & 1) ret = ret * x % mod;
x = x * x % mod;
k >>= 1;
}
return ret;
}
int n, l[MAXN], r[MAXN], p[MAXN << 1], N;
int f[MAXN][MAXN << 1], C[MAXN];
signed main() {
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> l[i] >> r[i];
p[++N] = l[i], p[++N] = ++r[i];
}
sort(p + 1, p + N + 1);
N = unique(p + 1, p + N + 1) - p - 1;
for(int i = 1; i <= n; i++) {
l[i] = lower_bound(p + 1, p + N + 1, l[i]) - p;
r[i] = lower_bound(p + 1, p + N + 1, r[i]) - p;
}
l[0] = 1, r[0] = N + 1;
for(int i = 1; i <= N; i++) f[0][i] = 1;
for(int i = 1; i <= n; i++) {
for(int j = l[i]; j < r[i]; j++) {
int len = p[j + 1] - p[j];
C[1] = len;
for(int k = 2; k <= i; k++)
C[k] = C[k - 1] * (len + k - 1) % mod * power(k, mod - 2) % mod;
for(int k = i - 1; k >= 0; k--) {
(f[i][j] += f[k][j + 1] * C[i - k] % mod) %= mod;
if(j < l[k] || j >= r[k]) break;
}
}
for(int j = N - 1; j > 0; j--) (f[i][j] += f[i][j + 1]) %= mod;
}
int ans = f[n][1];
for(int i = 1; i <= n; i++)
ans = ans * power(p[r[i]] - p[l[i]], mod - 2) % mod;
cout << ans << endl;
return 0;
}
