题意
地板有 $n$ 行 $m$ 列,一个机器人被安置在坐标 $(r_b, c_b)$,还有一个障碍位于 $(r_d, c_d)$。
每过一秒,机器人的坐标会 $(r, c)\rightarrow (r+d_r, c+d_c)$。
初始时 $d_r=d_c=1$,当机器人到达边界后,$d_r,d_c$ 会变化:
- 若机器人碰到上/下边界($r=1$ 或 $r=n$),下一秒 $d_r\leftarrow -d_r$,
- 若机器人到达左/右边界($c=1$ 或 $c=m$),下一秒 $d_c\leftarrow -d_c$.
每一秒内,位于 $(r,c)$ 的机器人有 $\frac{p}{100}$ 的概率,成功清理掉位于第 $r$ 行和第 $c$ 列的障碍,之后,它将按照上面的规则进行移动。
若每次清理的结果相互独立,求清理掉障碍物 $(r_d, c_d)$ 所需的期望时间。
题解
参考了由 darkkcyan 提供的 Codeforces Round #763 (Div. 2) Editorial。
首先,设 $\overline{p}=1-\frac{p}{100}$,代表不成功的概率。可以发现,机器人的轨迹会形成一个循环。
样例一
从样例一开始分析。

循环共两步,设 $x_1$ 表示机器人从 $(1,1)$ 出发的答案,$x_2$ 表示从 $(2,2)$ 出发的答案。
当位于 $(1, 1)$ 时,如果成功,花费时间 $0s$;若否,走到 $(2,2)$ 需要 $1s$,之后还需要 $x_2$,所以有:
\begin{cases}
x_1=p\cdot 0 + \overline{p}(1+x_2)=\overline{p}(1+x_2)\\
x_2=p\cdot 0 + \overline{p}(1+x_1)=\overline{p}(1+x_1)\\
\end{cases}
$$
联立一下,得到关于 $x_1$ 的方程:
x_1=\overline{p}(1+\overline{p}(1+x_1))
$$
逐层展开求解,$x_1$ 就是题目所求的答案。
样例二
再看样例二。
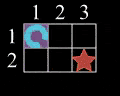
循环共四步:$(1,1)\rightarrow (2,2)\rightarrow (1,3)\rightarrow (2,2)$,其中 $(1,1)$ 不可能清除障碍,其余位置均有可能。
同理,设 $x_1$ 表示从 $(1,1)$ 出发的答案,$x_i$ 表示从循环第 $i$ 步出发的答案。(注意 $x_2\neq x_4$,它们的方向不同)
与样例一类似地,有:
\begin{cases}
x_1 = 1 + x_2\\
x_2 = \overline{p}(1 + x_3)\\
x_3 = \overline{p}(1 + x_4)\\
x_4 = \overline{p}(1 + x_1)\\
\end{cases}
$$
联立,得到关于 $x_1$ 的方程:
x_1=1 + \overline{p}(1 + \overline{p}(1 + \overline{p}(1 + x_1)))
$$
做法
若我们已知循环共有 $k$ 个点,且已知其中每个点的坐标,则可以列出像上面那样的方程组。
联立后的方程形如:
x=a_1(1+a_2(1+a_3(1+\cdots a_k(1+x)\cdots)))
$$
其中 $a_i\in\{1,\overline{p}\}$,是系数。当循环中第 $i$ 步可以清除障碍时 $a_i=\overline{p}$,否则 $a_i=1$.
由于数据范围 $4\leq n\cdot m\leq 10^5$,我们可以直接暴力搜索找到循环。
求解方程时,考虑从内向外逐层展开,过程中记录:常数项 $u$、一次项系数 $v$。
初始 $u=0$,$v=1$,每次展开时先算出 $a$,之后 $\begin{cases}v\leftarrow a\cdot v\\u\leftarrow a\cdot (u+1)\end{cases}$ 就可以了。
循环长度
我们把机器人的移动,分解在 $x/y$ 方向分别看。在一维的投影上,它们的周期分别为 $2(n-1)$ 和 $2(m-1)$.、

因此,$4(n-1)(m-1)$ 一定是 $\operatorname{lcm}(2(n-1), 2(m-1))$ 的整数倍,是循环长度的整数倍。
所以不必通过暴力搜索找到循环,对于所有数据都直接迭代 $4(n-1)(m-1)$ 次即可。
代码
注意倒序。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int mod = 1e9 + 7;
inline int power(int x, int k) {
int ret = 1;
while(k) { if(k & 1) ret = ret * x % mod; x = x * x % mod; k >>= 1; }
return ret;
}
inline int inv(int x) { return power(x % mod, mod - 2); }
int T, n, m, ax, ay, bx, by, dx, dy, p, pp;
signed main() {
cin >> T;
while(T--) {
cin >> n >> m >> ax >> ay >> bx >> by >> p;
pp = (100 - p) * inv(100) % mod;
p = p * inv(100) % mod;
int u = 0, v = 1;
dx = dy = -1; //倒序
for(int cas = 1; cas <= 4 * (n - 1) * (m - 1); cas++) { //迭代4(n-1)(m-1)次
if(ax + dx > n || ax + dx < 1) dx = -dx;
if(ay + dy > m || ay + dy < 1) dy = -dy;
ax += dx; ay += dy;
u = (u + 1) % mod;
if(ax == bx || ay == by) u = u * pp % mod, v = v * pp % mod;
}
cout << u * inv(mod + 1 - v) % mod << endl;
}
return 0;
}